2010廣州中考數學試題及參考答案、詳細知識點分析

25．（2010廣東廣州，25，14分）如圖所示，四邊形OABC是矩形，點A、C的坐標分別為（3，0），（0，1），點D是線段BC上的動點（與端點B、C不重合），過點D作直線＝－＋交折線OAB于點E．

（1）記△ODE的面積為S，求S與的函數關系式；

（2）當點E在線段OA上時，若矩形OABC關于直線DE的對稱圖形為四邊形OA₁B₁C₁，試探究OA₁B₁C₁與矩形OABC的重疊部分的面積是否發生變化，若不變，求出該重疊部分的面積；若改變，請說明理由.

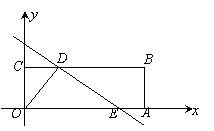
【分析】（1）要表示出△ODE的面積，要分兩種情況討論，①如果點E在OA邊上，只需求出這個三角形的底邊OE長（E點橫坐標）和高（D點縱坐標），代入三角形面積公式即可；②如果點E在AB邊上，這時△ODE的面積可用長方形OABC的面積減去△OCD、△OAE、△BDE的面積；

（2）重疊部分是一個平行四邊形，由于這個平行四邊形上下邊上的高不變，因此決定重疊部分面積是否變化的因素就是看這個平行四邊形落在OA邊上的線段長度是否變化．

【答案】（1）由題意得B（3，1）．

若直線經過點A（3，0）時，則b＝

若直線經過點B（3，1）時，則b＝

若直線經過點C（0，1）時，則b＝1

①若直線與折線OAB的交點在OA上時，即1＜b≤，如圖25-a，

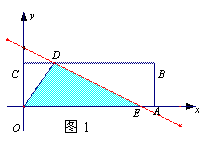
   此時E（2b，0）

∴S＝OE·CO＝×2b×1＝b

②若直線與折線OAB的交點在BA上時，即＜b＜，如圖2

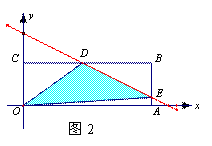
此時E（3，），D（2b－2，1）

∴S＝S_矩－(S_△OCD＋S_△OAE＋S_△DBE)

＝ 3－[(2b－1)×1＋×(5－2b)·()＋×3()]＝

∴

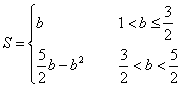
（2）如圖3，設O₁A₁與CB相交于點M，OA與C₁B₁相交于點N，則矩形OA₁B₁C₁與矩形OABC的重疊部分的面積即為四邊形DNEM的面積。

本題答案由無錫市天一實驗學校金楊建老師草制！

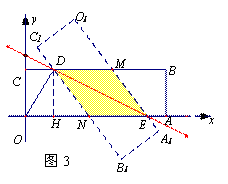
由題意知，DM∥NE，DN∥ME，∴四邊形DNEM為平行四邊形

根據軸對稱知，∠MED＝∠NED

又∠MDE＝∠NED，∴∠MED＝∠MDE，∴MD＝ME，∴平行四邊形DNEM為菱形．

過點D作DH⊥OA，垂足為H，

由題易知，tan∠DEN＝，DH＝1，∴HE＝2，

設菱形DNEM 的邊長為a，

則在Rt△DHM中，由勾股定理知：，∴

∴S_{四邊形DNEM}＝NE·DH＝

∴矩形OA₁B₁C₁與矩形OABC的重疊部分的面積不發生變化，面積始終為．

      【涉及知識點】軸對稱 四邊形 勾股定理

【點評】本題是一個動態圖形中的面積是否變化的問題，看一個圖形的面積是否變化，關鍵是看決定這個面積的幾個量是否變化，本題題型新穎是個不可多得的好題，有利于培養學生的思維能力，但難度較大，具有明顯的區分度．

【推薦指數】★★★★★

2010廣州中考數學試題及參考答案下載

上一頁  [1] [2] [3] [4] [5] [6] 

2016年中考信息不斷變化,www.txjunshi.com 91中考網提供的中考成績查詢查分、錄取分數線信息僅供參考，具體以相關招生考試部門的信息為準！