2016最新中考動態
2016中考錄取分數線
2016中考成績查詢、中考查分
2010廣州中考數學試題及參考答案、詳細知識點分析
作者：佚名 信息來源：本站原創 更新時間：2011-1-17
23．（2010廣東廣州，23，12分）已知反比例函數y＝
(m為常數)的圖象經過點A（－1，6）．
（1）求m的值；
（2）如圖9，過點A作直線AC與函數y＝
的圖象交于點B，與x軸交于點C，且AB＝2BC，求點C的坐標．
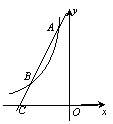
【分析】（1）將A點坐標代入反比例函數解析式即可得到一個關于m的一元一次方程，求出m的值；（2）分別過點A、B作x軸的垂線，垂足分別為點D、E，則△CBE∽△CAD，運用相似三角形知識求出CE的長即可求出點C的橫坐標．
【答案】解：（1）∵ 圖像過點A(－1，6)，
． ∴
（2）分別過點A、B作x軸的垂線，垂足分別為點D、E，
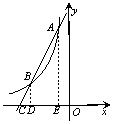
由題意得，AD＝6，OD＝1，易知，AD∥BE，
∴△CBE∽△CAD，∴
．
∵AB＝2BC，∴
∴
，∴BE＝2．
即點B的縱坐標為2
當y＝2時，x＝－3，易知：直線AB為y＝2x＋8，
∴C(－4，0)
【涉及知識點】反比例函數
【點評】由于今年來各地中考題不斷降低難度，中考考查知識點有向低年級平移的趨勢，反比例函數出現在解答題中的頻數越來約多．
【推薦指數】★★★★
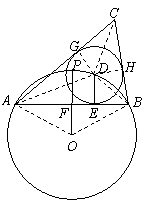
24．（2010廣東廣州，24，14分）如圖，⊙O的半徑為1，點P是⊙O上一點，弦AB垂直平分線段OP，點D是
上任一點（與端點A、B不重合），DE⊥AB于點E，以點D為圓心、DE長為半徑作⊙D，分別過點A、B作⊙D的切線，兩條切線相交于點C．
（1）求弦AB的長；
（2）判斷∠ACB是否為定值，若是，求出∠ACB的大小；否則，請說明理由；
（3）記△ABC的面積為S，若
＝4
，求△ABC的周長.
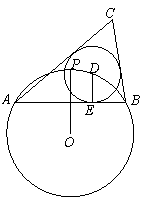
【分析】（1）連接OA，OP與AB的交點為F，則△OAF為直角三角形，且OA＝1，OF＝
，借助勾股定理可求得AF的長；
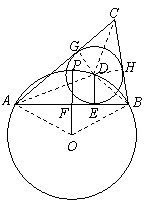
（2）要判斷∠ACB是否為定值，只需判定∠CAB＋∠ABC的值是否是定值，由于⊙D是△ABC的內切圓，所以AD和BD分別為∠CAB和∠ABC的角平分線，因此只要∠DAE＋∠DBA是定值，那么CAB＋∠ABC就是定值，而∠DAE＋∠DBA等于弧AB所對的圓周角，這個值等于∠AOB值的一半；
（3）由題可知
＝
DE (AB＋AC＋BC)，又因為
，所以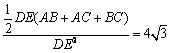
，所以AB＋AC＋BC＝
，由于DH＝DG＝DE，所以在Rt△CDH中，CH＝
DH＝
DE，同理可得CG＝
DE，又由于AG＝AE，BE＝BH，所以AB＋AC＋BC＝CG＋CH＋AG＋AB＋BH＝
DE＋
，可得
＝
DE＋
，解得：DE＝3，代入AB＋AC＋BC＝
，即可求得周長為24
．
【答案】解：（1）連接OA，取OP與AB的交點為F，則有OA＝1．
∵弦AB垂直平分線段OP，∴OF＝
OP＝
，AF＝BF．
在Rt△OAF中，∵AF＝
＝
＝
，∴AB＝2AF＝
．
（2）∠ACB是定值.
理由：由（1）易知，∠AOB＝120°，
因為點D為△ABC的內心，所以，連結AD、BD，則∠CAB＝2∠DAE，∠CBA＝2∠DBA，
因為∠DAE＋∠DBA＝
∠AOB＝60°，所以∠CAB＋∠CBA＝120°，所以∠ACB＝60°；
（3）記△ABC的周長為l，取AC，BC與⊙D的切點分別為G，H，連接DG，DC，DH，則有DG＝DH＝DE，DG⊥AC，DH⊥BC.
∴
＝
AB•DE＋
BC•DH＋
AC•DG＝
(AB＋BC＋AC) •DE＝
l•DE．
∵
＝4
，∴
＝4
，∴l＝8
DE.
∵CG，CH是⊙D的切線，∴∠GCD＝
∠ACB＝30°，
∴在Rt△CGD中，CG＝
＝
＝
DE，∴CH＝CG＝
DE．
又由切線長定理可知AG＝AE，BH＝BE，
∴l＝AB＋BC＋AC＝2
＋2
DE＝8
DE，解得DE＝3，
∴△ABC的周長為24
．
【涉及知識點】垂徑定理 勾股定理 內切圓 切線長定理 三角形面積
【點評】本題巧妙將垂徑定理、勾股定理、內切圓、切線長定理、三角形面積等知識綜合在一起，需要考生從前往后按順序解題，前面問題為后面問題的解決提供思路，是一道難度較大的綜合題
【推薦指數】★★★★★
2010廣州中考數學試題及參考答案、詳細知識點分析
上一頁 [1] [2] [3] [4] [5] [6] 下一頁
2016年中考信息不斷變化,www.txjunshi.com 91中考網提供的中考成績查詢查分、錄取分數線信息僅供參考，具體以相關招生考試部門的信息為準！